A Few Quick Thoughts on Apple's "Illusion of Thinking" LLM Paper

Illusions of illusions of thinking, or, "why Apple's "Illusions of Thinking" Paper Isn't Fair to LLMs"

Note: this is a very rough analysis and I don’t fully do justice to either the Illusion of Thinking paper or Gary’s response. I may eventually come back to this topic and fill out a more complete response.

People keep sharing this new Apple paper about LLMs called “The Illusion of Thinking: Understanding the Strengths and Limitations of Reasoning Models via the Lens of Problem Complexity.” The basic summary of the paper is that LLMs fail at many types of puzzles, sometimes in unintuitive ways, and that as a result the benefits of ‘reasoning’ models may be overstated if not inaccurate. For example, LLMs struggle with Towers of Hanoi, a reasonably simple puzzle where the goal is to move a stack of disks in ascending order from one pile to another, one at a time.

The game starts in the top left, and the goal is to get to the bottom right by moving disks from one column to the next without ever stacking a larger disk on a smaller one. This kind of puzzle game is very similar to the “Farmer crossing the river” riddle.

Towers of Hanoi has a well known algorithm that you can use to solve it, and the Apple paper discusses how LLMs seem unable to recover that algorithm.

Folks like Gary Marcus take these results as obvious examples of LLMs being insufficient for AGI.

What the Apple paper shows, most fundamentally, regardless of how you define AGI, is that LLMs are no substitute for good well-specified conventional algorithms.

…

But anybody who thinks LLMs are a direct route to the sort AGI that could fundamentally transform society for the good is kidding themselves. This does not mean that the field of neural networks is dead, or that deep learning is dead. LLMs are just one form of deep learning, and maybe others — especially those that play nicer with symbols – will eventually thrive. Time will tell. But this particular approach has limits that are clearer by the day.

And several people have expanded on takes like Gary’s and gone on to say that “AI” is “just” pattern recognition, and as a result is completely different from what humans do.

A few people have asked me for my take, so here it is.

First, I think this whole debate is just semantics. I don't know a priori why we would define intelligence as being meaningfully different from pattern matching, or why Gary defines AGI to mean something other than what LLMs currently do.

It's worth asking what the point of a definition is. I could tautologically define intelligence as "a property unique to humans" and then we can wipe our hands of the whole debate and say that of course neural networks aren't intelligent since they aren't human. But this obviously feels lacking. It’s like saying “only humans can have souls.” Why?

Semantics debates are often just exercises in question begging, but there is such a thing as a ‘good’ definition’. Definitions serve a purpose! Words are meant to ‘carve reality at the joints,’ that is, to provide clear delineations that help accurately communicate the state of observed reality. And the reality is these models are increasingly indistinguishable from what people are capable of doing. “Intelligence” is often used as a general purpose word to describe "being good at things" so, of course, colloquially many people now say models are intelligent. Because they are good at things. And, in fact, they keep getting better at things! We keep putting barriers in front of them that we think they cannot do, and within a few months they leap over those barriers. I fully expect that someone will have a working Towers of Hanoi LLM by next year.

Personally, I’ve been open in my belief that current models are already AGI for any reasonable definitions of ‘artificial’ and ‘general’ and ‘intelligence’.

Second, I'm not particularly surprised that LLMs are bad at solving puzzles that require learning and consistently applying algorithms. You don't have to reach for puzzles like Towers of Hanoi, most models can't do simple addition of large numbers. The reason is straightforward: it is hard to “learn” the algorithm for addition (add the two numbers on the far right, carry the one if necessary, repeat) just from seeing a lot of examples of addition. But neural networks learn other kinds of circuits, and large neural networks are able to learn some kind of addition algorithm that looks more like modular addition. I think most ML practitioners know to leverage LLMs for fuzzy analysis, and have LLMs write code for symbolic or numeric analysis; the Apple paper is putting some additional rigor around that general intuition.

Does that mean the LLMs aren’t intelligent? Hard to say, but as a counter point I’m not sure I could derive the formula for addition just by looking at symbols. Remember that LLMs aren’t taught like children, they don’t “learn” numbers. The only way they learn about the world is reading text!

Can you figure out what algorithm this is just from looking at it? Answer at the bottom.

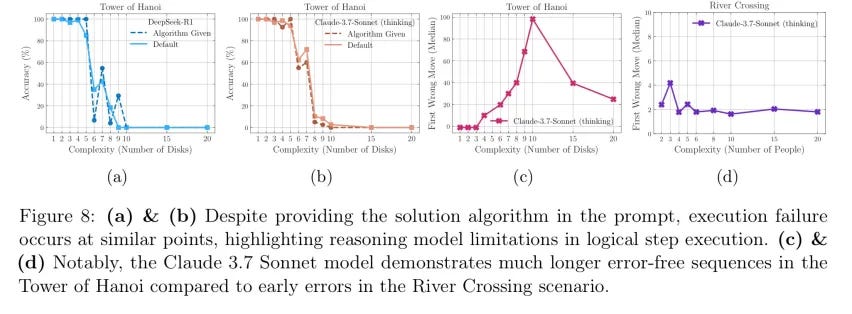
Of course, the next obvious thing to test is what happens if you actually give the model the algorithm. Does that result in the model doing better? In theory it should, the model no longer has to ‘recover’ the algorithm from examples.

And in fact the Apple researchers do exactly that, and they find the model does somewhat better but still eventually collapses.

But even this is not a slam dunk against LLMs!

Imagine I asked you to add two numbers with a billion digits each by hand. You presumably know the algorithm for adding things. But do you think, somewhere in those billion additions, you might make a mistake? To solve a puzzle like Towers of Hanoi, you need to a) know the algorithm and b) successfully execute it. But even people are not good at consistently executing algorithms! This is why we built computers! And to that point, LLMs can easily write code to solve Towers of Hanoi. I can ask Claude to do it and it will spit out the result in < 30 seconds.

Credit to Gary, he calls this out, though he quickly dismisses it:

The weakness, which was well-laid out by anonymous account on X (usually not the source of good arguments) was this: (ordinary) humans actually have a bunch of (well-known) limits that parallel what the Apple team discovered. Many (not all) humans screw up on versions of the Tower of Hanoi with 8 discs.

But look, that’s why we invented computers and for that matter calculators: to compute solutions large, tedious problems reliably. AGI shouldn’t be about perfectly replicating a human, it should (as I have often said) be about combining the best of both worlds, human adaptiveness with computational brute force and reliability. We don’t want an “AGI” that fails to “carry the one” in basic arithmetic just because sometimes humans do. And good luck getting to “alignment” or “safety” without reliabilty.

Then let the LLMs write code in your evals! You can have your cake and eat it too if you just let the LLM write code when it has to deal with problems that require computational brute force and reliability.

Here is Claude’s implementation of a 10 disk Towers of Hanoi, complete with a little UX to go with it.

The prompt for this is “Write code to solve a ten-disk towers of hanoi”. Note that the UX is flipped, i.e. the larger disk is always on top.

---

I think a lot of folks who don’t like LLMs are very sloppy in how they evaluate LLMs. Folks like Gary will seamlessly switch between “LLMs should behave in fuzzy ways like humans” and “LLMs should have the rigor and precision of a computer.” This seems unfair — we don’t expect humans to do both of these things.

I think of LLMs as fresh-out-of-college English-major intern. Anything I would expect of an fresh-out-of-college intern with a background in English, I would expect of an LLM. As they say, all models are wrong, some are useful — I’ve found this to be a very accurate heuristic for where LLMs succeed and where they fail. Would I expect my friend who is an incredibly talented creative writer to derive and then execute the algorithm for a 10 disk Tower of Hanoi? No, not any more than I would expect someone to be able to derive the solution to a Rubik’s Cube just by looking at it. Some people can, and good for them, but this is not a reasonable test of anything in particular.

That’s not to say the paper is bad. The Illusions of Thinking paper is actually really interesting, because it is a narrow exploration of where reasoning models fail and where reasoning models can be improved. But I think they dramatically overstate their conclusions when they say that these results point to “fundamental barriers to generalizable reasoning”, and that in turn has fueled a lot of bad pop-science interpretations that differ dramatically from what the paper actually says.

It would be a mistake to assume that because some models display some failure modes today, that no models can solve these problems in the near future. And it is absolutely wrong to assert that these models cannot transform society, especially since they already obviously have done so to anyone paying attention.

---

The algorithm is the Fibonacci sequence. Each number is mapped 1:1 with a shape and color. The shapes and colors are totally arbitrary, but that is the point — an LLM has no prior understanding of what a ‘token’ is. The arbitrary nature of representing symbols as above is intentionally meant to put you in the frame of what an LLM ‘sees’. How many examples of addition using this mapping would you need before you could figure out an algorithm for addition?