Ilya's 30 Papers to Carmack: Complextropy

This post is part of a series of paper reviews, covering the ~30 papers Ilya Sutskever sent to John Carmack to learn about AI. To see the rest of the reviews, go here.

Paper 1: The First Law of Complexodynamics

High Level Summary

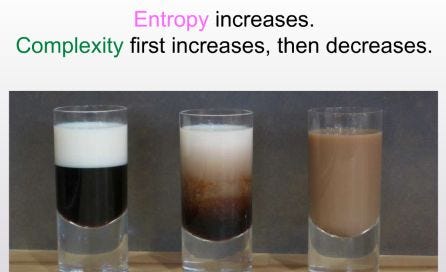
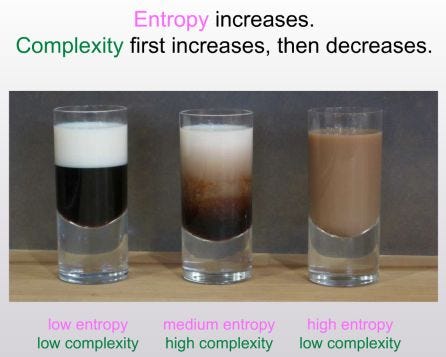
These two pictures basically explain the entire post.

Most of the post is about defining this ‘law of complexity’. Aaronson goes into a fair bit of information theory speculation. He concludes that a good representation of ‘complextropy’ is the “the length of the shortest computer program that describes, not necessarily x itself, but a set S of which x is a “random” or “generic” member”, subject to certain computational constraints. This is also known as ‘Sophistication’, derived from Kolmogorov Complexity.

As far as I can tell, Aaronson is working backwards from observation to theory. The article was published in 2012 — I was curious to see if anyone had provided further empirical evidence justifying the theory. For example, systems where we can precisely describe the complexity using Aaronson’s definition, that match up with some observed quantifiable ‘complexity’ in the state of the system.

I found this tweet. This medium post. And that’s about it. Looks like it was never really picked up elsewhere, at least not that I can tell.

Insights

There’s something intuitive about the idea that systems become more complex before they become less complex, even as they gain entropy. I think this is because the ‘manifold’ of entropy has a bunch of minima and maxima. In other words, as you gain entropy, you may end up creating some structures that are higher entropy than the baseline condition, but still lower entropy than the highest possible entropy state. I feel like I’ve seen similar properties outside of coffee cups, especially in biology — this paper reminded me of enzymes acting as a catalyst to make some process occur. You need the enzyme (structure) to go from a low entropy state to a high entropy state (pre to post chemical reaction).

Still, even if I bought the core idea, at first glance, I was kind of unsure why this paper was in Ilya’s 30. Don’t deep learning models get more complex, even by the time they are done training?

Actually, no! My recent new favorite paper is Toy Models of Superposition by Anthropic. It is a BEAR of a paper. Really long. But take a look at this figure:

This figure shows that as a model tries to represent more and more features, it begins to take on complex structure in its underlying embedding space. It starts without any structure, and ends with every feature touching every other feature. Both of these are not very complex. And then in the middle you get all of these weird patterns — tetrahedrons and triangles and digons and square antiprisms. Sounds pretty complex to me!

I feel like after reading this paper, I started seeing the pattern described in a lot more places. But then again, this may just be confirmation bias.