Ilya's 30 Papers to Carmack: RNN Regularization
This post is part of a series of paper reviews, covering the ~30 papers Ilya Sutskever sent to John Carmack to learn about AI. To see the rest of the reviews, go here.
Paper 4: Recurrent Neural Network Regularization
High Level
Models exhibit a lot of different failure modes. One particularly common failure mode is 'overfitting'.
Overfitting is when a model picks up on, essentially, noise in the training data. It over specializes to that noise, which makes it useless 'in the wild'. For example, imagine I was training a hotdog/no-hotdog image classifier. If I only trained the model with images taken from my Pixel 7, I might find that the model doesn't work with pictures taken from an iPhone! That's because the model 'overfits' on 'noise' in the training set — in this case, the hyper-specific camera parameters of my phone. Here's a longer (probably apocryphal) example of why this may be a problem.
This leads to a sort of counter intuitive insight: we actually want to make our model worse on the training set so it can generalize to the test set!
How can you make your model worse?
Well, one easy way is to just make it smaller. A smaller model has less 'representational capacity'. And on the flip side, for any given training set, you could make an infinitely large model that just memorizes the whole set. In other words, there is a deep connection between model size and overfitting. But generally we don't want to make the model smaller. The last 20 years of deep learning research have shown pretty conclusively that bigger models trained on bigger datasets do better! So assuming we don't want to kill representation capacity, what else can we do?
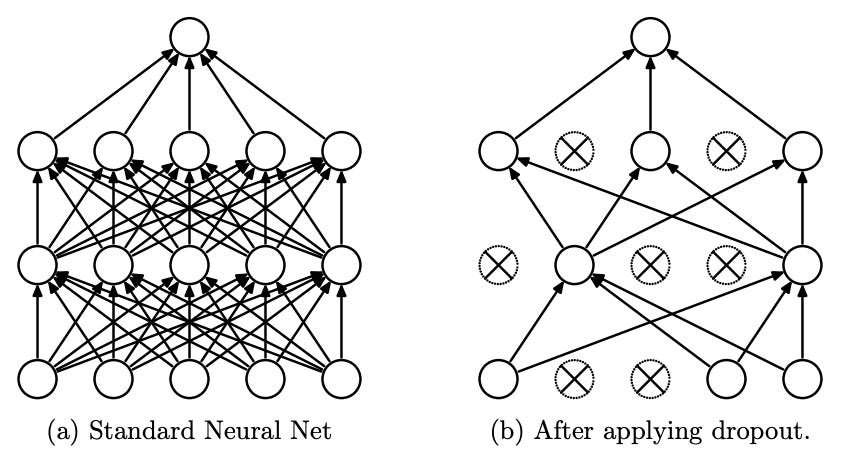
One thing we can do is 'simulate' a smaller model by arbitrarily removing some of the weights at each step of training.
If I have a model with 100 neurons, at each step I could 'turn off' 50 of them randomly. We call this 'dropout'. In some sense, this is like having a smaller model. It forces the model to learn independent relationships. A model without dropout can learn N^2 relationships. A model with dropout learns significantly less. Empirically, dropout works really well!
Except in RNNs.
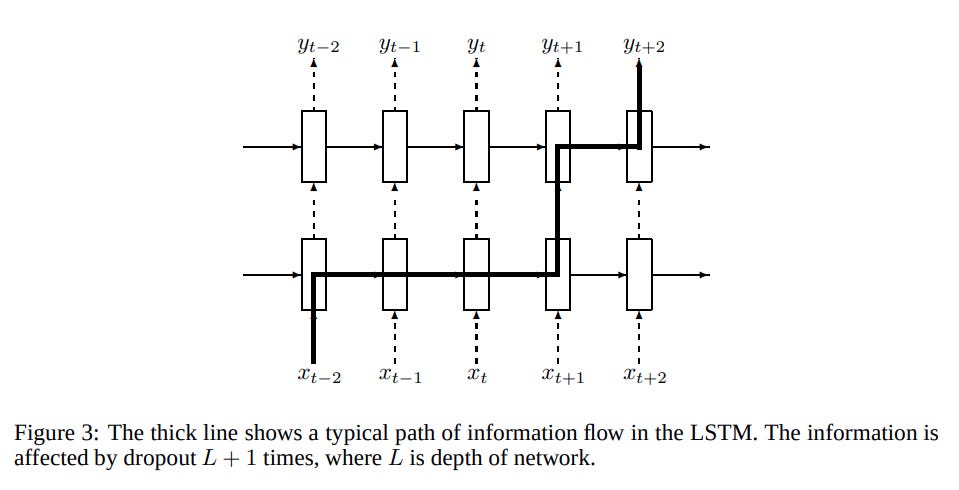
This paper figures out how to make dropout work for RNNs. The basic idea is that previously, everyone was applying dropout to every layer in the model. That also included connections between timesteps. This paper discovered that applying dropout everywhere except the hidden state dependency worked really well.
Annnnd that's basically the whole paper!
Insights
In some sense, this should be really obvious. Dropout is a form of signal corruption — you are taking some signal and removing some of the data arbitrarily. If you apply dropout between timesteps on an RNN, you are effectively repeatedly applying noise to the same signal. Over a long enough sequence, you'll actually just lose all of the original signal. The noise (dropout) will wipe it out. RNNs already struggle with learning long term dependencies, dropout makes it way worse. And as a result, the model will just learn not to depend on that signal. During training the model will basically ignore the hidden state, effectively making the RNN a worse feedforward network.
More generally, it's interesting to see how model’s learn to prioritize or deprioritize information during training. If you can squint you can just sort of grasp at why the model works better with dropout in this setting than in the ‘default’ setting. It feels like there should be some theory here, some kind of ‘theory of optimization’. That intuition is what a lot of deep learning practitioners learn to rely on.
One last miscellaneous thought: I’ve always wondered whether there was a theoretical equivalence between smaller models and models with dropout. Is there a model of size X that is equivalent to some larger model of size Y with dropout Z? Naively, a vector of size N can have N * N dependencies. During dropout, the representational capacity is something less than N * N. Solve for the equivalence.
This is still a naive take. Even if you could just ‘solve for the equivalence’, you’d be missing the fact that during inference you have all neurons present (see this stack exchange post for more details). And just based on inspecting the model, dropout vs smaller-model are two completely different functions/architectures. Still, from an information-representation perspective, there is some relationship there…