Simple DL Part 2: Embeddings
December, 2020
[Originally from my website]
In my opinion, you need to understand embeddings to really 'get' deep learning. Embeddings are the magic fairy dust that power every deep learning model, from ImageNet to GPT-3. I think in embeddings. Embeddings are the foundation for any intuition I have about DL, so all of my future posts in this series are going to refer back to the embedding concept.
Because this is important foundation, I'll be splitting this section into two parts. The first section tries to define embeddings, while the second part explains why they work.
TLDR
Embeddings are stores of information represented as a list of floats (a float vector).
Float-vectors are unique because they are continuous, which means we can think of them like points on a map (or, more generally, points on an N-dimensional surface).
A good embedding is one where similar information is 'close' to each other in our map.
Because embeddings are lists of floats that represent concepts, we can turn concepts into computation.
A deep learning model is made of a stack of embeddings. Embeddings are constrained by the input data (features) and the loss function.
The features limit what the embeddings can learn, and the loss tells the model what to prioritize. Models are as good as their features and as bad as their loss.
We can improve a model's performance by changing the features, the architecture, or the loss function. These change the embeddings, which changes the underlying information map.
Simple DL Part 2a: What are Embeddings?
Embedding Basics
Ok now for the long version. We'll start with a definition: an embedding is a list of numbers (AKA a float vector) that represents some information. You can have embeddings for just about any kind of information out there. There are word embeddings. There are sentence embeddings. There are image embeddings. There are graph embeddings. There are furniture embeddings. Basically, if you can think of a concept, you can represent it as an embedding.
If you're more mathematically minded, the embedding wiki page has a pretty good formal description/definition of embeddings. The core idea is that an embedding is a mapping between some object (or space) X to some object (or space) Y, such that the 'important' structure of X is preserved. For most deep learning applications, we care about embeddings in metric spaces.
Information vs Format
This is already kinda weird. How can we take any concept and represent it as a list of numbers? To really grasp this idea, we need to remember that information is not the format. This is a core principle of information theory and underpins most of modern computer science. Basically, we can take a piece of information and represent it in any format, and the underlying information won't be any different. We might lose information in the conversion process, but that's due to practical limitations of the format.
An example may help nail all this down. Let's say we have a picture of my wonderful dogs, Sparky and Lego.
There is a lot of 'information' in this picture. Can we convert that 'information' to text without losing any of it? We could try describing the image. "Two dogs" captures most of the information. "One small brown dog and one medium-sized gold dog on a slate grey surface" captures even more. We can keep going like this, with ever more complex descriptions -- a picture is worth a thousand words, after all.
Can we do better? "Two dogs" captures a lot of the information, but its just 8 characters. Information has a compression limit; 8ch is simply not enough data storage capacity. It will always leave something out. Instead, lets go pixel by pixel and write out the colors. Starting from the top left, we could write "grey, grey, grey, light grey, light grey, grey, grey...". Not exactly Hemingway, but it would be a perfect representation of the image. We would capture all of the information.
The leap to an embedding is straightforward. Replace our words/colors with RGB values -- something like [(128, 128, 128), (128, 128, 128)...]. Flatten that out, and we've successfully turned our image into a numeric vector that perfectly captures all of original information.
What about text? Can we turn text into an embedding? Well, one strategy could be to turn every character into a unique number, like ASCII. This is why a numeric sequence like 104 101 108 108 111 32 119 111 114 108 100 can be read as 'hello world' by a computer. If we had a really long sequence of text, like a book, we could instead turn every unique word into a unique number. So even though we started with text, we can pretty easily convert to a numeric representation.
Ok so hopefully by now you have some intuition for what an embedding is. Question: is [0.124, 458.2356, 85.3, 2.01] an embedding? Or is it a random list of numbers?
We need to make a small change to our initial definition.
An embedding is a list of numbers (AKA a float vector) that represents some information, as well as a mechanism for encoding and decoding that float vector to something useful. In the examples above, our encoding/decoding scheme was RGB or ASCII. In deep learning, our encoder/decoder is the Deep ML model.
Conclusions
Embeddings are a super unintuitive concept, and I think to really reason about them you have to clear two huge hurdles. Figuring out information vs. format was one of those hurdles -- once I could separate the abstract concept of data from the format it was presented, I began to think in terms of flowing information. And information as a concept is really something that can only live in your head. Data is converted from bits on a disk to pixels on a screen, which is interpreted as lightwaves by our retinas, which is converted electrical signals in our brain...ALL of that is format. The actual information is abstract, existing in a void that cannot ever be actually materialized.
Ok enough poetry.
This section covered how information can be represeneted in a bunch of different formats. In the next section, we'll cover the second big hurdle: how embeddings can be used to convert concepts to computation. We'll talk about why different formats matter, and what we can do with embeddings that make them so powerful for Deep ML.
Simple DL Part 2: Why do we care about Embeddings
Recap
In the previous section, we defined an embedding as a float vector representation of information that, for practical purposes, comes with a mechanism for encoding/decoding the data. We talked about how information was not the format, and how you could perfectly represent information in a bunch of different ways. And we had a few examples of how images and text can be represented as embeddings. In this section, we dive into why embeddings are powerful and key to understanding deep learning.
Format Matters
Why do we bother with a float vector in the first place? If we can "perfectly represent information in a bunch of different ways", why lists of numbers? The boring answer is that computers can operate on numbers really easily. The more interesting answer is that different formats let you manipulate your data in different ways.
Float vectors are continuous representations. You can compare them. You can add them together. You can average them. You can do all these neat mathematical operations on them to quickly and efficiently shift your data around. And this is really powerful, because you can turn concepts into computation.
Let's say we wanted to represent two concepts: gender, and royal status. We can represent these as axes on an XY coordinate plane, so that any coordinate [X, Y] corresponds to a gender/royal status pairing.
With this rough coordinate system, we can embed words by mapping them into x-y values. For example, we might say the word King is mapped to coordinates [1, 1]; the word Queen is mapped to [-1, 1]; the word Man is mapped to [1, 0]; and the word Woman is mapped to [-1, 0].
Now we can do some really cool stuff. We could average words together to find other words near their conceptual midpoints. We could subtract words to remove their meaning, or add words together to search for specific related concepts. We could add new dimensions, like a Z-axis for 'Age'. We can quantify words and use math to analyze them. That, to me, is magic.

We can do all of this magic because float vectors correspond really well to geometry. People aren't great at remembering lots of numbers, but we do a great job with spatial reasoning. Embeddings allow us to turn concepts into points in space, where we can visualize things like 'distance' or 'surfaces'. When I think about creating a model to embed cars, I imagine a fantasy map where different regions represent specific car makes and models. You have a Mercedes town, which is pretty close to BMW-burg , and kinda far from the Bus-ville. If our map does a good job keeping similar things close to each other, we've solved 90% of the deep learning problem.

Imperfect Information
With infinite resources, we could perfectly convert any piece of data from one format to another. That's neat, but also just about useless. Most of the time, we care about removing information, filtering important data from noise. This is especially true in deep learning, where a hotdog image classifier might be taking in thousands of pixel values and returning only a single bit.
Embeddings go hand-in-hand with information compression -- the challenge of a good embedding is to figure out what the important information is. Our map doesn't need to draw every tree and mountain in high resolution detail, but it does need to make sure the borders are in the right spot.
But how do we compress information?
So far we've been isolating the axes of our embedding -- we have a 'gender' dimension, and a 'royalty' dimension, and maybe an 'age' dimension, and they don't mix at all. This makes it easy to draw a map, but the map isn't going to carry a lot of info. To work with larger data, we need to get rid of axes and look at regions. Instead of saying "+Y = royalty", we would say "the area around coordinates [0, 1] is associated with royalty". Notice how we are defining the region with both coordinates. As we walk around our coordinates, we're 'exploring' the feature space. This gives us much more freedom to represent different concepts.

Because we can slice our float vectors all sorts of ways, we can create millions of semantic combinations that a human would never be able to remember or process. Luckily, we don't need to -- neural networks do it for us. When a deep model is training, it's learning how to draw a super high dimensional map at each layer. And, it can mix and match input data in all sorts of arbitrary ways to figure out where the imaginary lines should be, and which concepts should be close to other concepts. Then, during inference, the model reads the map back on some new data point to see what's nearby, and use the map to make decisions.
Features, Embeddings, and Losses: Making a Model
Wait. How does a deep model decide where the imaginary lines should be? What does it mean for concepts to be 'close together'?
Let's take a step back. Every deep learning model is composed of three parts: the features, the embeddings, and the loss function. A "feature" is just a fancy way of saying input data. And the embeddings are the pieces of the model itself -- every deep model is basically just a stack of embeddings.
We'll dive into loss functions in more depth later, but for now think of the loss function as the thing that the model is trying to solve. If you have an image recognition task, for example, the loss will be a measure of how good the model is at recognizing objects in images. During training, the model manipulates the stack of embeddings based on the features and loss.
Each embedding is trying to draw a map based on the information provided by the input features. If we want to identify vehicles, the embedding-map needs to have a clear border between busses and sports cars. If we want to classify text, the embedding-map needs to be able to separate a frown from a smile. And, if a human can't figure out how to draw a reasonable separation boundary for a few data points...well, you probably want to think about your problem and your data some more.
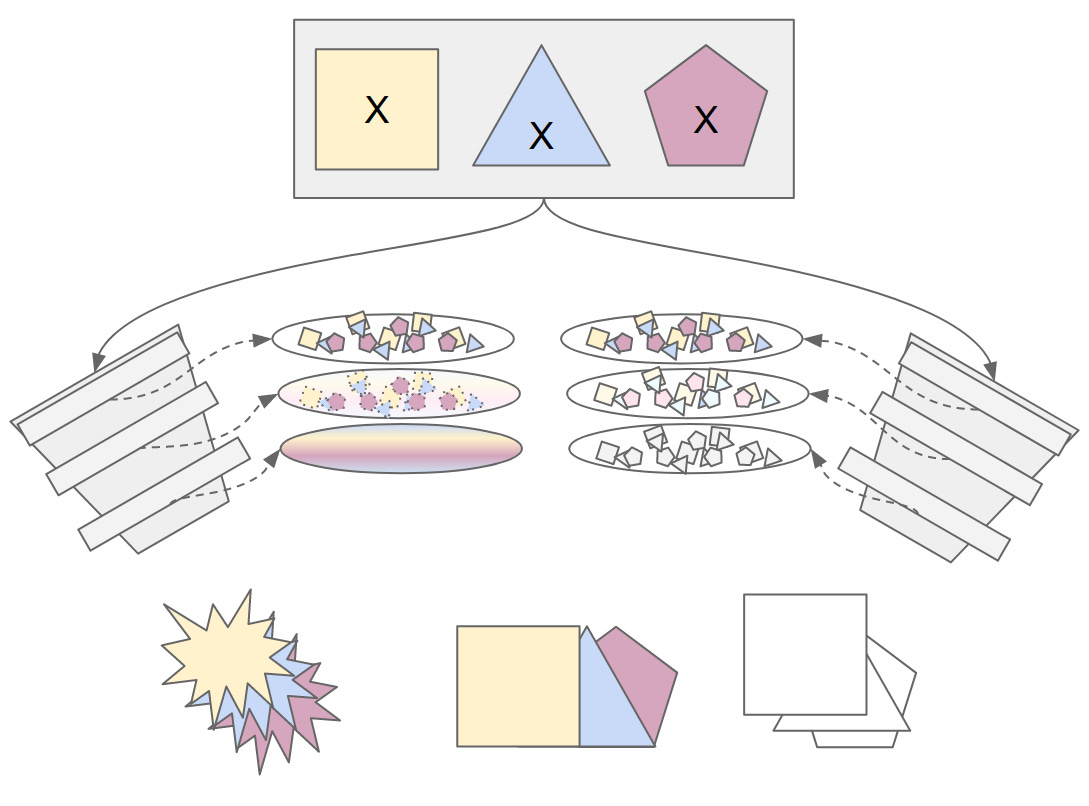
Let's ground this in a specific example. Say I'm the embodiment of $SELF_DRIVING_CAR_COMPANY and I want to create an ML model that identifies NYC taxis, because NYC taxis behave erratically on the road. NYC taxis are bright yellow. So, to improve model outcomes, I could remove all other colors EXCEPT for yellow in my input features; or, I could tweak my loss function to have the model predict color as well as whether or not there is a taxi. Reducing the color input gives the model less data to work with, ensuring that our embeddings will have more of the color information we care about. Adding color to the loss encourages the model to retain color information in the underlying embedding-map.
Overall, the features and the loss function constrain the embeddings. Embeddings can only represent information that is provided in the initial feature set. And the embeddings remove (or emphasize) information based on the loss function. In my head, it's like sculpture -- the features are the clay, the loss is the final vision, and the backpropagating gradients chip away or add to the embeddings so that they are they right shape and size.
I think this gets at why Deep ML models are so powerful. You can throw any features and any loss function into the thing, and the inner embeddings will find a way to connect the inputs and outputs. There's also a corollary to this: your models will only ever be as good as your features and as bad as your loss.
I like this framing because it also gives us some insight in how we can change our models so they do what we want. There are really only three levers: we can add new or more features, to try and give the model more to work with; we can change up the architecture, to try and influence how the underlying embeddings mix and match data; or we can modify the loss(es), to sculpt the underlying information as it flows through the model. Each of these approaches has trade offs. Adding more features will always help the model, but getting new data is really hard. Changing the architecture in a useful way requires a stroke of inspiration or dumb luck. And modifying the loss is highly volatile.
There's one other cool thing about this framing. If we're ever confused about what our model is doing, we can take our model embeddings and plot them in 2D, like an actual map. This will let us see whether similar concepts are appearing close or far away. We'll get into debugging models down the line, but Google 'TSNE plots' if you're curious.
Conclusions
This post was so long it already got split in two, and we're starting to move away from embeddings alone, so I'll leave off here.
There are probably other ways to reason about deep learning, but for me the embedding concept is absolutely critical. When I think about deep models, I need to visualize how information flows through the embeddings I've constructed. Over the rest of the series, we're going to try this visualization process with a bunch of popular architectures -- Convolutions, LSTMs, GANs, Graph Neural Networks, Transformers, and more. And hopefully in the process, you'll get a bit more intuition for how deep learning works.
Homework Answers
There's no right answer! Some parts of the embedding space display coherent semantic proximity -- for example, dogs, cats, and puppies are all close to each other. But other parts of the space aren't really that reasonable -- why are navigational tools next to politics? In general, the conceptual space is way too complex to represent in two dimensions, so whether or not this is a good embedding depends entirely on the problem you are trying to solve.







