Ilya's 30 Papers to Carmack: LSTMs
This post is part of a series of paper reviews, covering the ~30 papers Ilya Sutskever sent to John Carmack to learn about AI. To see the rest of the reviews, go here.
Paper 3: Understanding LSTMs
NOTE: for this paper, I found it easier to combine the 'high level overview' and 'insights' sections into one long analysis.
Many of the papers in Ilya's set of 30 refer to LSTMs. Most of them just assume LSTMs are the default kind of RNN. And, for the most part, they are — even in 2024 the most exciting RNN papers are really LSTM papers.
In many cases you can basically abstract over an LSTM. You don't really need to know how it works in order to use it as a recurrent block in a model. And that's what many papers do — they rarely go into detail about what an LSTM is. That said, if you're trying to grok deep learning, it's pretty useful to understand why an LSTM is different from and better than the previous kinds of RNNs. The best deep learning practitioners have a deep intuition for what kinds of information processing these models are doing. Exploring LSTMs and why they work can help build that deeper intuition.
So without further ado, what is an RNN vs an LSTM?
An RNN is a 'recurrent neural network' — essentially, a neural net with a loop in it. The loop allows the model to maintain state. There's a lot of ways to think about this state. You can think of it as a 'scratch pad' that the model can read and write from. You can think of it as a 'message' that is being passed to the next iteration of the model. You can think of it as the model providing input to itself.
This additional loop is really valuable when tryng to represent things that are inherently sequential, like lists or sentences. As the model processes each element in the sequence, it can learn a representation of the prefix (the data it has seen thus far) which can guide how it processes the next step. We'll talk more about why this is really cool when we discuss the Unreasonable Efficacy of RNNs blog post (paper 2 on Ilya’s list).
RNNs in their most basic form — a single loop — have a big problem. The model doesn't "know" what information it might need at each future step. So, as a sequence gets longer, the model has to pack more and more information into the 'message' that is passed from one time step to the next. But it only has a fixed vector size with which to do so, and there is a limited amount of computation capacity in the single layer of weights that are used to update the state. At some point, the model runs into information theoretic limits. This in turn makes it hard to represent long range dependencies.
One way to fix this problem is to make the model 'smarter' about what information it stores. Consider a sentence "The quick brown fox jumped over the lazy dog". By default, an RNN will 'weight' each word equally; that is, every word has an equal opportunity to modify and 'pack' information into the shared state. But, like, do we really need the model to store a bunch of information about the word "the"? And maybe there are some sentences where we really want to store a lot of information about the word "fox", and others where we don't care at all. It would be nice if the model could update its state a bit more 'intelligently'.
LSTMs to the rescue.
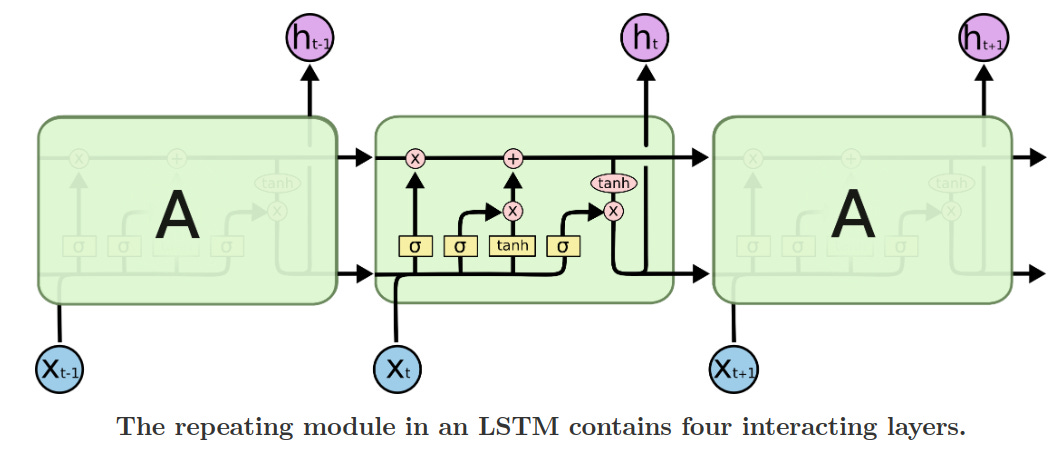
The basic idea of an LSTM is to lean into the 'scratchpad' model of RNN state. If you were writing a program that could read and write to disk, you might want some way to decide when you read from the disk, what you read from the disk, and what you write back to the disk. The LSTM encodes those key behaviors as vector operations.
The core of the LSTM is the 'state'. The default behavior of the state is to just pass itself along, without modification.
If the model wants to change the passed along state, it has to create a vector that actually does the modification.

This is a big difference from the default RNN pattern, which requires the state to be modified by a learned weight matrix every timestep.

In other words, in the default RNN, the model has to write to the scratch pad every single step, and it has to somehow incorporate information from the current input. In an LSTM, the model can choose what information to 'write' to the scratch pad — it may write nothing at all.
How does this actually work in a weights-and-vectors sense though?
You should think of a deep neural network as having representations (vectors) and computation (weights). The LSTM takes in a representation of the current input X — i.e. a vector that contains relevant information about X — and a representation of the previous state H. It runs these both through a set of weights. Obviously, these weight matrices are in a literal sense just linear algebra. But in a computational sense, these learned weight matrices 'figure out' what information to keep, what information to forget, and what information to overwrite. That information gets stored into a 'state update' vector, which then gets applied to the state with simple vector math.
I want to quickly go on a tangent about these weights. Unfortunately as a field, we don't really have the theory to describe these weight matrices (and the computation they learn) in a more rigorous way. Sometimes, models don't learn the right patterns. Or the model's weights blow up in some way during training. Or the model learns to be hyperspecific to one set of input and not to others. So clearly it is not the case that every LSTM successfully learns these 'keep/forget/overwrite' computations. There is some intuition around model architecture at play here — the specific architecture of the LSTM makes it more likely that the model will learn the computations we care about. And, in a more general sense, all of deep learning is about finding architectures that are more likely to result in the computations we care about. The default RNN model potentially has the ability to learn the same kinds of computation that an LSTM can. They are theoretically equivalent in representation capacity1. But it is much harder for the RNN to do so, the architecture itself makes it very difficult.
That said, what's funny about LSTMs is that it turns out some parts of the architecture may not matter that much! There's some theoretical motivation for when to use a sigmoid and when to use a tanh, or when to use vector addition or vector multiplication. But there are also a ton of variants of LSTMs that all seem to work about as well as each other! They all share one basic property — they 'learn an update to apply to the state', instead of updating the state directly2.
More generally, one lesson to take away from LSTMs is that we should aim to increase model capacity by 'separating concerns'. In the default RNN, there is only one weight vector and one hidden state representation. The model has to put everything into that constrained space. You could make the weights/vectors really big, but that may actually decrease the likelihood that the model will learn useful things — it may end up learning spurious correlations between 'behaviors' and 'state'. By separating out the update from the state, the model has to learn these two things in isolation. That in turn results in a much more narrow/focused 'space' of things the model can do, making it more likely that the model will land on the 'correct' computation.
More broadly, the universal approximation theorem states that even a single-layer feed-forward MLP can represent any function given a large enough hidden state. And yet, we obviously don’t just use giant MLPs everywhere! Just because something can learn a function doesn’t mean it will.
For folks who know a lot about diffusion models, this should sound familiar! The core innovation of diffusion models was to learn state updates instead of learning the state directly.