This post is part of a series of paper reviews, covering the ~30 papers Ilya Sutskever sent to John Carmack to learn about AI. To see the rest of the reviews, go here.
Paper 12: Multi-Scale Context Aggregation By Dilated Convolutions
High Level
This is another one of those classic papers, where some really basic / standardized procedure that everyone knows in 2024 is introduced for the first time.
Back in 2016, there had been a bunch of progress on image classification, and deep learning models were far and away the best automated classifiers. The same could not be said for image segmentation. The former is about taking an image and deciding what category it should be in. It is, fundamentally, a bucketing problem. The latter is about taking an image and deciding which pixels correspond to which objects. This is significantly harder.
Why is it harder?
Learning segmentations implicitly learns classifications. If you can identify exactly which pixels in an image represent a hotdog, you can also answer the question of whether the image shows a hotdog at all (This is likely how most humans do classification — that is, via segmentation). But the opposite isn't true. A model can confidently tell you that a hotdog is present in an image, without being able to convey where the hotdog is.
Another way to think about these problems is that they occur on different resolutions. Classification is all about decreasing resolution. You start with a HxWx3 input vector (an RGB image) and need to reduce the resolution down to a vector with D categories. So you can use pooling and subsampling layers. At each resolution decrease step, you only need to retain the important information for the classifier at the end; you can throw away anything else.
But with semantic segmentation, you can't reduce the resolution — you have to keep the pixel level information in the model all the way through to the end, to be able to output pixel masks — but you also have to reduce the resolution in order to get an understanding of where the hotdog starts and ends. Your model needs to somehow compile all of the information of the image, and apply its understanding of the image to each pixel separately. Some papers attempt to solve this paradox by using downsampling followed by upsampling; others attempt to provide multiple versions of the same image at different scales as input to a model.
In this paper, the authors attempt to approach the problem sideways. They ask: is it possible to get both global AND local context without scaling the resolution down at all?
Introducing dilated convolutions.
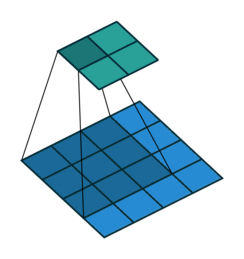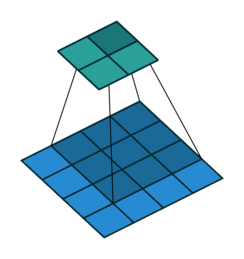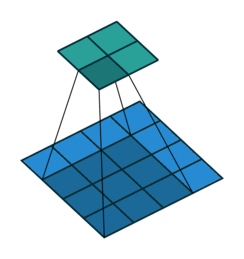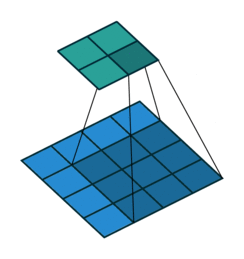
To understand dilated convolutions, we need to understand regular convolutions. Everyone who has ever worked with convolutional networks knows about convolution animations. Here is the basic one for standard convolution networks.
The core idea behind a convolutional network is that images have structure that can be exploited — pixels are strongly related to nearby pixels in predictable geometric ways. To learn that structure, we "slide" a "filter" of weights over the image, summing up the values in each NxN section to get a single value for that filter at each "patch" of the input. You can run multiple filters at the same time. Each filter learns something different, so the output number for each has a different meaning; and the results are stacked on top of each other, resulting in "dimensions" associated with each filter. The output embedding is going to be smaller in terms of height and width, but often has more "channels" — one for each filter in the layer before. In other words, you get a single embedding vector that represents a particular geographic patch of the image, per geometric patch, laid out to match the input geometry.

The problem with a standard convolution layer is that depth is expensive. You generally don't want to train convolutional layers with a single filter, because that filter acts as a massive bottleneck for signal. But as you increase the number of filters, the number of channels also increases, resulting in increasingly large matrix multiplications. And the filters themselves only increase their "context window" linearly, resulting in way more computation for large images. To make this computationally feasible, most deep convolutional networks decrease resolution as they go deeper. The model mixes information across patches, resulting in a more global understanding of an image at the cost of the local, per pixel understanding (helped along by pooling and sampling).
But, as mentioned earlier, you need that per pixel understanding for segmentation tasks.
Here is what the animation looks like for a dilated convolution.
The basic intuition is simple — just expand the input field by N, for an N-dilated convolution. This allows the model to retain an understanding of a wider window at significantly less computational cost. If you stack dilated layers, you get an exponential increase in the "coverage" of a single filter, which in turn means you need fewer layers overall to manage large images. With more efficient compute per patch, the authors are able to train segmentation models that do not lose per pixel resolution (the output is the same size as the input) while still pulling together global context (because the exponential increase in window size means each output pixel has the appropriately full image as input).
Insights
One way to think about semantic segmentation is that you are trying to do a simple classification for each pixel of an image, with the full image as input. "Given every pixel as input, is this particular pixel part of a hotdog?" If you have an image of size HxW, you are effectively doing HxW classifications. Dilated convolutions give you a pretty cheap way to get full-image locally-sensitive embedding representations for each pixel. Once you have the per-pixel embeddings, you can just do classification the normal way — feed it through a softmax layer and do a cross entropy loss.
This also points to a potential failure mode of dilated convolutions. You don't actually get the full image as input to every pixel. Rather, you get some smattering of nearby pixels in a window around the input pixel. The structure of the dilated convolution means that there is potential to lose some data in the gaps of the dilation.

More generally, the dilated convolution is likely not exploiting the geometric structure of an image as effectively as a regular convolution.
On a different note, one thing I never really poked at before was the relationship between convolution filters and attention heads.
In a Transformer, you have these QK matrices that together learn how to structure an NxN attention matrix, where each word in a sequence attends to other words in the sequence. You can imagine that your attention head might learn how to model adjectives by putting high attention weight on the associated noun. Or maybe your attention head will learn 'lookbacks', where each instance of a proper noun attends to the first time that proper noun appears. These are really cool 'programs' to learn! And it's obvious how they would be useful, and in fact some Transformer research shows that these attention heads do explicitly learn programs like this. The problem is that each attention head can only learn one such program. In a traditional Transformer, you get around this by having multiple attention heads at each layer. Each one can learn something totally different.
This is exactly like filters in a convolutional network. Each filter has the ability to pick up on some specific pattern. Maybe one filter picks up on edge detection, while another picks up on color change, while a third picks up on contrast differences. The more filters you have, the more flexibility your model has to learn different programs that each influence the final result.
In the paper, the authors mention that the dilated convolutional networks struggle when they are randomly initialized. They end up settling on using identity as their initialization — that is, each layer starts by passing the input signal through without modification. This reminds me of the value of identity in ResNets. There, the theory was that layers that represent identity allow signal to pass more easily through different parts of the network. I suspect the same intuition applies here: you are trying to do a dense prediction (a per-pixel classification) so it makes sense to start with the assumption that you need to pass each per-pixel signal down to the end of the model. Identity initialization allows you to start with all of your input signal intact at the beginning of training, and the model can selectively lose or modify that signal over the course of the training regime. If the model starts with random initialization, there is no signal that is passed all the way through the model to start. More generally, it's likely easier to learn small changes on an identity function that defaults to signal propagation, than it is to learn signal propagation from scratch. The same logic also applies to LSTMs.
Though dilated convolutions are really valuable, they ironically ended up NOT becoming the default model for image segmentation. In 2024, Meta's Segment Anything Models primarily rely on Vision Transformers. Transformers natively learn a graph over an input sequence — they are able to decide based on the input whether to focus on local or global information for a given token. For images, this means that individual patches of an image can learn to 'attend to' other patches in the same image. This is perfect for semantic segmentation, where each patch (and eventually each pixel) needs both local and global information.