This post is part of a series of paper reviews, covering the ~30 papers Ilya Sutskever sent to John Carmack to learn about AI. To see the rest of the reviews, go here.
[EDIT: this one was accidentally sent out after the identity mapping review. I ended up just publishing both of them at the same time]
Paper 11: Deep Residual Learning for Image Recognition
High Level
In 2024 it seems weird that anyone ever doubted the scaling hypothesis. But it's called a 'hypothesis' for a reason — before ~20201, there was bitter contention over whether models would always get better as they got bigger, without diminishing returns.
Part of the reason for this contention was the significant difficulty in actually training larger models. The history of training larger and larger models is one in which the industry would knock down some massive, seemingly insurmountable blocker, only to find a larger, even more insurmountable blocker behind it. First there were all sorts of issues with overfitting — see my review of Minimum Description Length. Then, the industry had to deal with limited chip memory and multi-chip training — see my review of AlexNet. Then it turned out that really large models suffered from vanishing or exploding gradients, caused by repeated application of the chain rule2 — this eventually got solved by better normalization methods like BatchNorm.
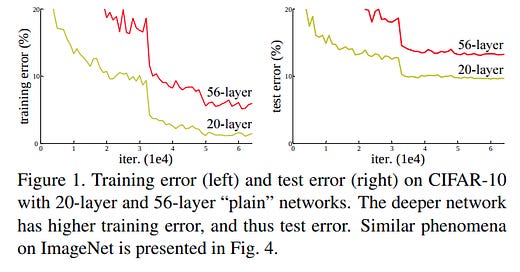
By 2015, a new problem had cropped up: bigger models would often simply perform much worse.
This is obviously bad. But it's also unintuitive. Take a look at that graph again. The 56 layer model performs worse than the 20 layer one. Let's assume that you actually can't do better than 20 layers, the 20 layer CIFAR-10 model is optimal for that dataset. The 56 layer model should be able to exactly replicate the 20 layer model — trivially, the 56 layer model could learn the first 20 layers exactly, and then the rest of the layers are just identity layers (i.e. multiply everything by an identity matrix, 36 times). But even though this trivial solution exists, the model seems incapable of learning it.
The authors call this 'the degradation problem'. The existence of the degradation problem implies that identity solutions in particular are hard for models to learn — the model must end up adding some noise.
My own theory is that learning explicit matrices is always hard. An identity matrix consists of 1's along the diagonal and zeros everywhere else. In a standard sgd backpropagation learning scheme, it's very difficult to drive a set of numbers to this exact format. One reason why this may be true is because gradients are calculated over minibatches. This means that in order to drive a matrix to exactly identity, all of your minibatches must also drive to identity. Over enough batches you will eventually converge to approximately identity (within epsilon), but it will take a long time, and you will never get exactly there. Since there will always be epsilon error in each layer, that error will compound the more layers you have.
This naturally leads to the question: if traditional models can't learn identity, can we craft a model that can? One plausible way out is to try to learn 'residuals'.
In slightly more formal terms, a stack of layers F(x), can learn any function3. We want the model to learn H(x). But this may be 'hard' for the model to learn. The model should equivalently also be able to learn H(x) - x. This may be 'easier' for the model to learn than H(x). So we can modify our model architecture to simply add x at the end of the learned block. Now the model only has to learn F(x) = H(x) - x. And the final output of the layer is still H(x)4.
Hopefully it's easy to see why this network block could more easily learn an identity function — in order for the ResNet block to represent identity, the learned parameters F(x) only have to learn 0. And the use of ReLu activations means the weight layer simply has to be negative. Any negative matrix will suffice. The model has a much higher affordance.
The authors train a big model with residual connections, and of course, things turn out great. I don't normally care for the empirical results in ML papers because they are so often cherry picked, but I feel like this paper is the exception:
ResNets have lower error at virtually every part of the curve. They converge faster and better, even at smaller model sizes. And there's no additional parameter cost — you are simply getting more bang for your buck. This is a fantastic empirical result. This paper is one of the few where the authors legitimately reason their way to a better, more optimal model in every setting.
Aside from benchmark accuracy, the authors also show a small but important interpretability result: the model layers in the ResNet have significantly lower standard deviations on their per-layer responses than their plain counterparts. Further, larger ResNets have lower standard deviations than smaller ResNets. This is loose empirical evidence that the basic motivation for ResNets is true: the model really does learn a less 'intrusive' operation that is closer to 0.
Insights
There is a type of deep learning paper in which the authors discover that models of a certain form struggle to learn a class of representations. The architecture itself makes learning this class difficult. So the authors try to change the architecture to improve results on that class of problem specifically, without degrading general performance in other settings and without significantly improving parameter count5. The ResNet paper is the gold standard in this category. It's an incredibly simple modification that results in no changes in overall parameter count of the model, and has clear and obvious empirical benefits across basically every learning task. Unsurprisingly, residual connections become a staple in every model architecture from here on out.
Since publication, there's been a lot of theorycrafting around why ResNets are so much better. Some of it focuses on what the model has to learn — in particular, learning an update is easier than learning an entire state. Some of it focuses on how signal propagates through a model — in particular, these 'skip connections' make it easier for gradients to pass through the model in the backwards pass. Some of it focuses on representation capacity — in particular, residual connections massively increase a model's representation capacity because there is no longer a single bottle neck layer. All of these are likely true.
One connection I don't see made often is how similar ResNets are to LSTMs. An LSTM improves over a standard RNN by using a slightly more complicated 'gating' mechanism to learn state updates on a continuous stream of state. At each time step t, the model takes in some input and, instead of updating the entire state, learns an update that is applied to the state. A ResNet does virtually the same thing, except over depth instead of time. Much of the reasoning behind why ResNets are useful also apply to LSTMs and vice versa. It is likely very difficult for a 'standard' RNN to learn an identity function, but an LSTM would have a much easier time of it by simply setting gates to 0.
In practice, the main difference is that:
the LSTM gets some new input at each step, while the ResNet does not;
the LSTM shares weights at each step, while the ResNet does not
But these differences are somewhat superficial. You could easily construct a ResNet that gets additional input at each step or uses the same weights in multiple parts of the stack, and in fact this is roughly what some later models do.

This parallel is fascinating to me. Sequence learning had already switched to learning updates on a 'residual stream' with LSTMs. After this paper, learning updates on residual streams becomes the norm across the industry. It seems like a generally applicable rule that learning updates is always easier than learning state changes. Even more broadly, it seems like models learn representations and operations, and keeping these conceptually separate somehow makes learning dynamics significantly easier. But this is probably an article in its own right, so I'll leave off here.
If the gradient is < 1, repeated multiplications through layers would eventually drop to 0; if the gradient is > 1, repeated multiplications through layers would eventually explode to float-overflow.
See the Universal Approximation Theorem.
In theory you could add a weight matrix instead of using just identity, such that the model has to learn F(x) = H(x) - Wx but the authors stick with identity mapping. This is explored more in Paper 16.
The reason this matters is because we want to be confident that improvements in results come from the architectural changes, instead of just from having more parameters.