This post is part of a series of paper reviews, covering the ~30 papers Ilya Sutskever sent to John Carmack to learn about AI. To see the rest of the reviews, go here.
Also, welcome to all the folks who recently joined from Hacker News!
Paper 19: Relational Recurrent Neural Networks
High Level
Neural networks are universal function approximators. That means that a neural network can, with certain assumptions, approximate any function that exists. And it turns out that everything can be modeled as a function of some kind. Images are a function. Language statistics are a function. The stock market is a function.
The set of functions is infinitely large. And most of those functions don't actually represent anything useful. Like, I can have a function that outputs a bunch of squiggles on a 2D plane, but that is obviously less semantically coherent or interesting than a function that exactly outputs the batman symbol.
So we want our models to learn useful functions, which are a tiny tiny subset of the total amount of possible functions a model can learn.
How do we do that?
Well, one thing we can do is try to bias the model to learn specific kinds of functions using the model architecture. For example, when we look at an image, there is a clear geometric relationship between pixels; we know intuitively that pixels that are close together are related to each other. Convolutional networks are built to assume that pixel proximity matters. They are biased to learn functions that incorporate pixel proximity information. And of course RNNs and LSTMs have a different kind of bias. They are built to learn how some input at time t relates to t + 1. Now, anyone who has trained one of these models can tell you: there is no guarantee that a model will learn the function that you want just because the model architecture is biased in a certain direction. But it makes training significantly easier. And in some sense, the entire field of deep learning is about finding architectures that bias us towards general reasoning.
Before transformers took off, a lot of people really liked recurrent neural networks. The bias towards sequential data felt really useful; the auto-regressive generative properties of an RNN often produced output that looked quite a bit like reasoning over data that was learned over time. I think this is why every other paper that we've reviewed thus far is "some-other-model but stick an RNN on it". But as we discussed in the attention paper and the set2set paper reviews RNNs are too biased. An RNN assumes that the input is strictly sequential, but almost all interesting data has some non-sequential dependencies. Among other things, that makes relational reasoning really challenging. RNNs really only learn one relationship. They can't easily learn many-to-many relationships, and that really seems like a precursor to general reasoning.1
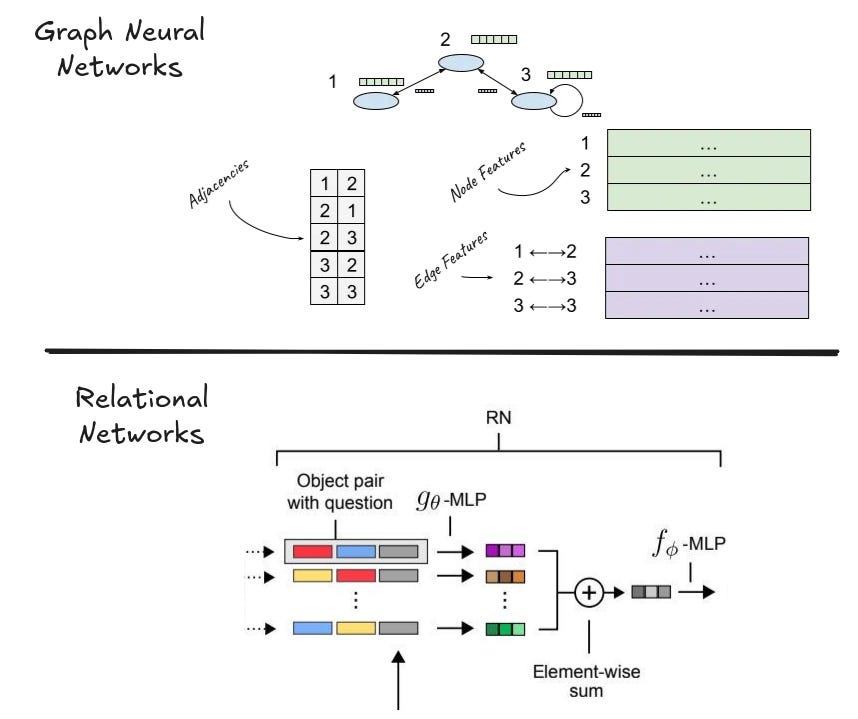
Of course, researchers did try to create architectures that would be biased towards learning relationships. We actually covered two papers in the space already. The first was the MPNN paper which attempted to learn representations over hard-coded graph relationships. And the second was the relational network paper, which used pairwise interactions between multiple object representations to do relational reasoning.
But these approaches are lacking, at least in the 'general intelligence' sense, precisely because they are not temporal. Neither of them have an effective mechanism for learning new things about the world — a significant limitation if we want to build AGI.
That brings us to this paper. The folks over at Deepmind are looking at the state of the art in various domains and ask themselves: can we create a model that "can learn to compartmentalize information, and learn to compute interactions between compartmentalized information"? And they pull inspiration from all over. They take the recurrence models of LSTMs, the representational relationships of relational nets, the memory slot architecture of neural turing machines, the temporal relationship building of normal attention mechanisms, and self attention from transformers to create…this thing.
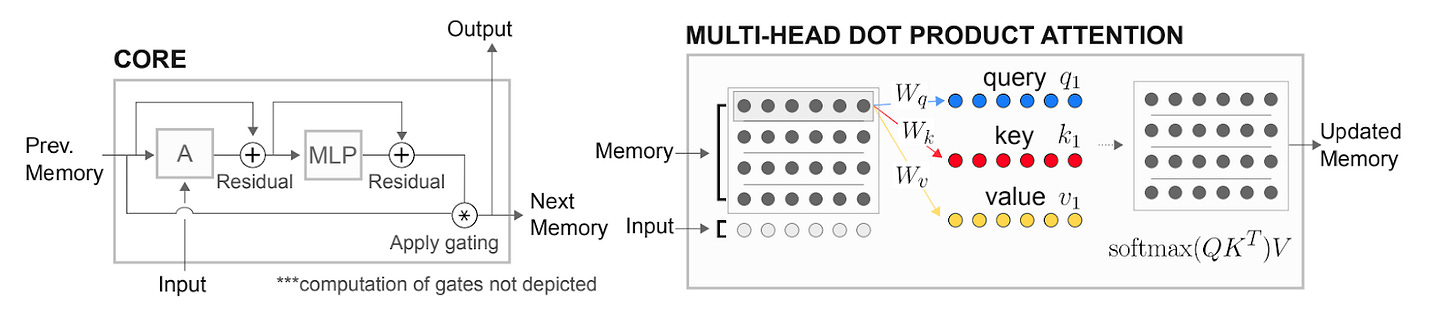
The authors call this a 'relational memory core'. I call it 'a transformer inside an RNN'.
The core idea here is to have a model that internally contains a set of 'memory slots', each which can contain a 'memory representation'. They want these 'memories' to interact with each other, and they want to create a mechanism to introduce new memories, so that the model can continually update its memory bank over time.
The 'memories interacting' part is pretty straightforward. Conveniently and obviously, the memory representations are just vectors, and as a result all of the slots together can be instantiated as a matrix. And a natural way to model pairwise interactions between rows in a matrix is through self attention.2 In the standard LLM setting, each token 'attends to' all of the other tokens and pulls in relevant information from those other tokens into its own representation. The authors cntrl-f the word "token", replace it with the word "memory", give some justification about why these embeddings are interchangeable3, and essentially call it a day.
The recurrence bit is a bit more interesting.
In transformers that model language statistics, you have token representations instead of memory representations, and the entire input is passed in at the beginning. LLMs pass these representation matrices from one transformer block to the next, and each transformer block learns a custom set of weights to modify the underlying token representations. The same basic idea happens in these recurrent relational networks. The main differences are:
At each step, you add some totally new input that the model has not seen before. The dimensions work out such that the final memory matrix spreads the new input vector across its memory slots.
Each set of weights is actually the same. So you're passing your 'memory matrix' through a set of weights that is shared across all steps. This likely regularizes what the model can learn — the model is limited to learning a more general set of operations that are valid across many different memories.
The new memory is actually learned as an update, that is then applied to the previous memory through a gating mechanism. It's unclear if this is actually better, though our previous reviews suggest it generally is.
Because RNN recurrence is computationally linear and constant in memory, the relational memory core will have a fixed size memory buffer, but can still scan over arbitrarily large sequences. In other words, it's an RNN with a more complicated update mechanism.
In the experiments, the authors do a bunch of language modelling and code execution experiments, which the model (obviously) does fine at. These are sorta uninteresting.
The authors also construct a fun little toy task called "Nth Farthest", where they feed in a sequence of vectors and ask: “What is the nth farthest vector (in Euclidean distance) from vector m?” A priori, I'd expect that this task is quite hard for most models. The right answer isn't readily available from the input alone, you can't just encode and retrieve information. Rather, the model has to actually reason about the distances between the vectors. Even in settings where the reference vector isn't yet present.
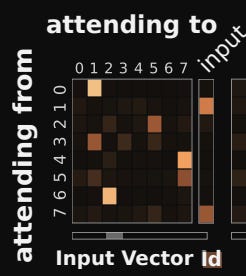
Attention analysis on the Nth Farthest task reveals some neat things about where the model 'focuses' depending on when it gets certain information. In particular, the model learns different attention patterns based on when the reference vector m is introduced. If the reference value is not present yet, the model essentially 'stores' the input into one or two memory slots.
Here, there is high attention weight for slot 7 and slot 1 on the input, and nowhere else. This will essentially result in the input V vector being 'written' to slot 7 and slot 1.
Once the reference vector is introduced, it gets read into a particular set of memory slots, and then all future inputs seem to mostly or only care about the relationship to those memory slots.
For example, the reference vector is introduced and 'read into' rows 2 and 4. And from that point on, the highest attention weights on all of the other steps is on 2 and 4.
What does this mean? No idea. And the authors say as much in the discussion: "and while the analysis of the model in the Nth farthest task aligned with our intuitions, we cannot necessarily make any concrete claims as to the causal influence of our design choices on the model’s capacity for relational reasoning, or as to the computations taking place within the model and how they may map to traditional approaches for thinking about relational reasoning." (This is, by the way, the best thing I have ever read in an ML paper)
Insights
I love how much the authors actually pull from other papers — they are really trying to grab a bit of everything that kinda works on their own to see if they all work better together. In some sense, that's been a bit of a theme of the series. I feel like half of these papers are "let's stick an RNN on it to make it better" in some form or another. But as we approach the end we start to see things that look a bit more familiar to modern practitioners, like self-attention.
Speaking of self-attention, even though I've been in this space for a long time I was unaware that other folks were trying things with self-attention beyond the standard transformer architecture. In retrospect, this makes sense — the original "Attention is all you need" paper really only became an industry-wide phenomenon after the GPT models cracked scaling.
Although 'cracked' may be a bit generous.
In the VLAE review I discussed the concept of research threads:
As I've read through this list of 30-ish papers, I've started categorizing different papers into threads. One paper might propose an idea and a different paper might pick it up a few years later, following a similar theme. These threads are rich conversations, with folks responding to and building upon each other's ideas.
If you've been paying attention to ML research over the last few years, you'd know that one of the more popular modern threads is "how do we deal with the fact that transformers suck at scaling?"
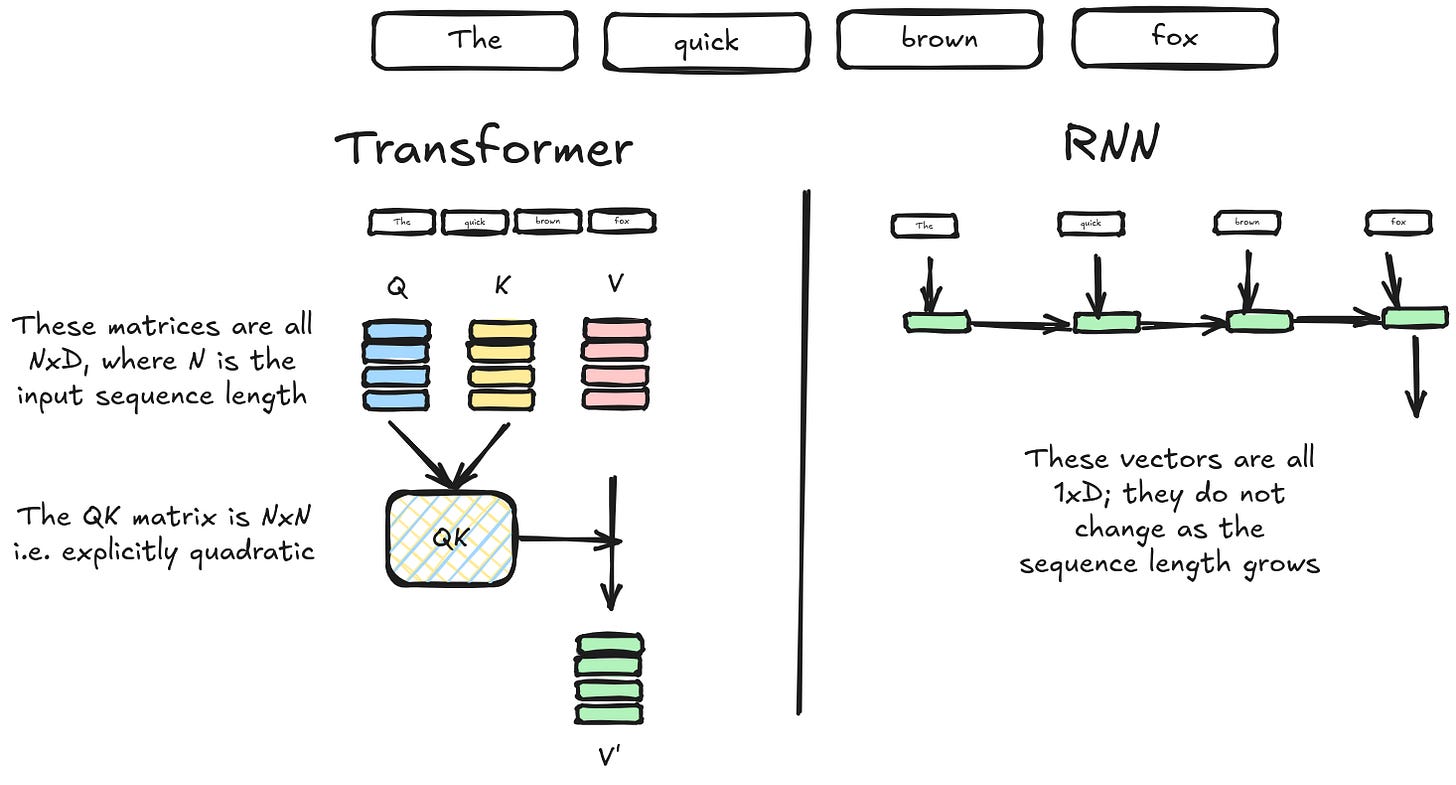
Even though transformers as an architecture have proven to be incredibly powerful general learners, they scale quadratically in compute and space as the sequence length of an input gets longer. And this is actually a general problem with attention — you have to store an increasingly large number of previous states to attend over all of them. Framed in terms of 'memory slots', you can think of the standard transformer as having a different memory slot per element in the sequence. That means the transformer 'memory' grows as the sequence length gets longer. Having a larger memory space for longer contexts is good, in that the transformer appropriately has more representation capacity when it needs it. But it also makes transformers extremely inefficient, especially compared to RNNs which scale linearly as a function of sequence length.
There are dozens of papers that are tackling the quadratic space / compute complexity problem. Linear Attention, Attention free Transformers, Flash Attention, Were RNNs all we needed?, and most recently, Titans. But Relational Recurrent Networks was first. In fact, one way to read the motivation behind this paper is that the authors recognized that transformers were too expensive to scale without massive compute clusters, and so attempted to use RNNs to manage the scaling issue. Storing memories in a recurrent way allows for theoretical 'infinite' scaling of attention, because there is no context window limitation. Many of the modern papers attempt to do something similar, by turning transformers into some kind of recurrence equation.4 So far this is an unsolved problem. But amusingly, the Titans paper actually reads somewhat similarly to Relational Recurrent Networks in its core concepts. There is nothing new under the sun.
The last thing I want to end with here is this quote again:
"We cannot necessarily make any concrete claims as to the causal influence of our design choices on the model’s capacity for relational reasoning, or as to the computations taking place within the model and how they may map to traditional approaches for thinking about relational reasoning. Thus, we consider our results primarily as evidence of improved function – if a model can better solve tasks that require relational reasoning, then it must have an increased capacity for relational reasoning, even if we do not precisely know why it may have this increased capacity."
Man, I love this quote, because it so perfectly captures the inherent fuzziness of working in deep learning. Going back to the beginning, the whole goal of architecture design is to try and bias these models towards learning certain kinds of "good" functions more efficiently than other kinds of "bad" functions. But there's no science here! The authors talk a big game about 'memory' and 'memory slots', but they have no idea about whether that is even a semantically coherent concept! At the end of the day, we really don't have any idea what these models are doing. We just kinda squint and say "yea, I think that should work", and sometimes it does and sometimes it doesn't.
There's something very 'empiricist' about all of this, which is why I have been so disdainful in the past of papers that have too much math in them. In a very real sense, the math is just a fig leaf, something required to get the papers published. The vast majority of these papers are "I think this should work, and the numbers show that it did". There just aren't many papers that make that clear, and I love the authors of this paper for just owning that they have no idea why their architecture actually works.
Part of the reason why everyone was so into attention from 2015-2020 is precisely because it was seen as a way to remove some of the biasing that RNNs naturally have to particular data flows. RNNs are extremely 'locally sensitive'. At each step, they only care about what is immediately nearby. RNNs with attention become more 'globally sensitive' because they can pull information in from anywhere in the sequence.
Note that self attention implementations traditionally learn a single weighting pattern between entities. This is sort of equivalent to learning a single convolutional filter. Often we want to learn more than just one kind of weighting pattern, so we use multiple attention heads. The authors do the same here, but for simplicity it's easier to just present as a single head.
At the end of the day, tokens, memories, objects, concepts — they are all represented as vectors. These models don’t really ‘care’ about what the input is once it gets put into some kind of vector space. That’s why neural networks are so powerful in so many different domains!
Often lossily — you can't go from quadratic compute to linear compute without approximating something somewhere!